揭秘扇形面积求解的奥秘
怎样求扇形的面积
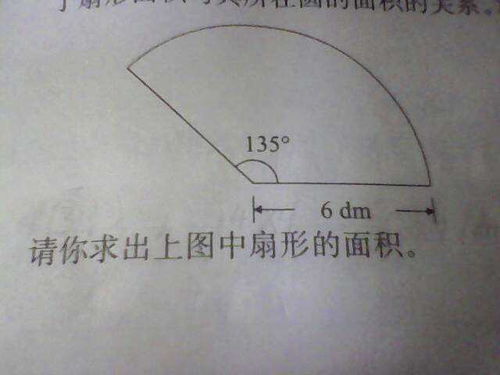
扇形是与圆相关的一种平面图形,它是圆的一部分,由圆的两条半径和它们之间的弧围成的封闭图形。在日常生活中,我们经常会遇到与扇形相关的面积计算问题,比如扇贝形的装饰品面积、某些圆形建筑的部分面积等。因此,掌握扇形面积的计算方法对我们的生活和工作都非常有帮助。
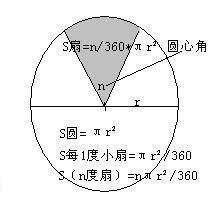
要求扇形的面积,首先需要了解几个基本概念:圆的半径(r)、圆心角(n)以及弧长(l)。这些参数在扇形面积的计算中起着至关重要的作用。
扇形的面积公式主要有两种形式,一种是基于圆心角的,另一种是基于弧长的。我们可以根据已知条件选择合适的公式进行计算。
一、基于圆心角的扇形面积公式
扇形面积与圆心角有直接的关系。一个完整的圆的圆心角是360度,如果扇形的圆心角是n度,那么扇形的面积占整个圆面积的比例就是n/360。根据这个比例关系,我们可以推导出基于圆心角的扇形面积公式:
扇形面积 = (n/360) × π × r²
其中,n是扇形的圆心角,r是圆的半径,π是圆周率,通常取3.14。
举个例子,如果扇形的圆心角是90度,半径是5厘米,那么扇形的面积就是:
扇形面积 = (90/360) × π × 5² = (1/4) × π × 25 ≈ 19.63平方厘米
二、基于弧长的扇形面积公式
除了圆心角,扇形的面积还可以通过弧长来计算。圆的周长是2πr,如果扇形的弧长是l,那么扇形的面积占整个圆面积的比例就是l/(2πr)。根据这个比例关系,我们可以推导出基于弧长的扇形面积公式:
扇形面积 = (1/2) × l × r
其中,l是扇形的弧长,r是圆的半径。
举个例子,如果扇形的弧长是6.28厘米,半径是4厘米,那么扇形的面积就是:
扇形面积 = (1/2) × 6.28 × 4 = 12.56平方厘米
在实际应用中,我们可能会遇到只知道扇形的圆心角和半径,或者只知道扇形的弧长和半径的情况。因此,掌握这两种扇形面积的计算方法是非常必要的。
接下来,我们来看一些扇形面积计算的注意事项:
1. 准确测量或给出参数:无论是圆心角、半径还是弧长,都需要准确测量或给出,否则会影响扇形面积的计算结果。
2. 选择合适的公式:根据已知条件选择合适的扇形面积公式进行计算。如果已知圆心角和半径,就使用基于圆心角的公式;如果已知弧长和半径,就使用基于弧长的公式。
3. 注意单位换算:在实际应用中,可能会遇到不同的单位,比如圆心角可能是度数,也可能是弧度;半径和弧长可能是米、厘米或其他单位。在进行计算之前,需要进行必要的单位换算。
4. 利用辅助工具:在进行扇形面积计算时,可以利用计算器、电脑等辅助工具来提高计算效率和准确性。
为了更好地理解和掌握扇形面积的计算方法,我们可以看一些具体的实例:
实例一:已知扇形的圆心角是120度,半径是3厘米,求扇形的面积。
解:根据基于圆心角的扇形面积公式,我们有:
扇形面积 = (120/360) × π × 3² = (1/3) × π × 9 ≈ 9.42平方厘米
实例二:已知扇形的弧长是4π厘米,半径是4厘米,求扇形的面积。
解:根据基于弧长的扇形面积公式,我们有:
扇形面积 = (1/2) × 4π × 4 = 8π ≈ 25.12平方厘米
除了上述的扇形面积计算方法外,我们还可以通过一些图形变换或几何关系来求解扇形的面积。比如,我们可以将扇形看作是一个三角形和一个圆弧的组合体,然后分别计算它们的面积再相加。但这种方法相对复杂且不准确,因此在实际应用中并不常用。
总的来说,扇形面积的计算是一个既基础又重要的知识点。它涉及到圆的性质、比例关系以及基本的代数运算等多个方面。通过学习和掌握扇形面积的计算方法,我们可以更好地理解和应用与圆相关的几何知识,为我们的生活和工作带来更多的便利和乐趣。
希望这篇文章能够帮助你更好地理解和掌握扇形面积的计算方法。如果你还有其他关于扇形或其他几何图形的问题,欢迎随时向我提问。我会尽我所能为你解答。
- 上一篇: 奥比岛探险指南:全面解析七色花寻找图文攻略
- 下一篇: 一键查询全国建筑人员证书信息
-
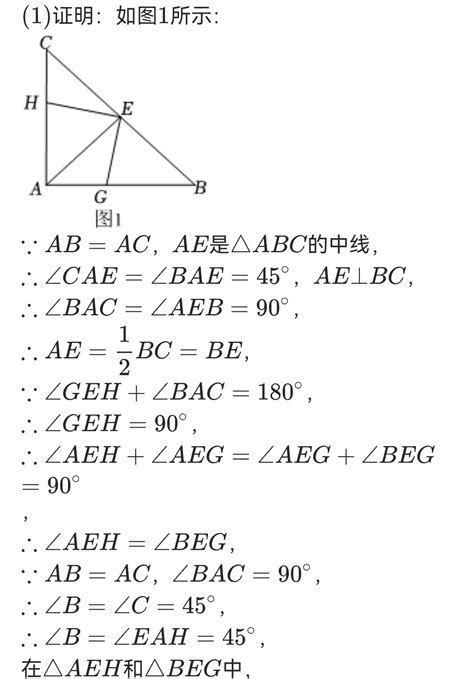 三角形ABC中AC边上的中线BD将周长分为12厘米的两部分,求解相关问题资讯攻略03-26
三角形ABC中AC边上的中线BD将周长分为12厘米的两部分,求解相关问题资讯攻略03-26 -
 揭秘:一次函数fx的表达式及其特性,f(f(x))=x+2求解过程资讯攻略03-26
揭秘:一次函数fx的表达式及其特性,f(f(x))=x+2求解过程资讯攻略03-26 -
 探索数学奥秘:十的阶乘究竟有多大?资讯攻略04-07
探索数学奥秘:十的阶乘究竟有多大?资讯攻略04-07 -
 全面解析:月亮的知识要点概览资讯攻略11-03
全面解析:月亮的知识要点概览资讯攻略11-03 -
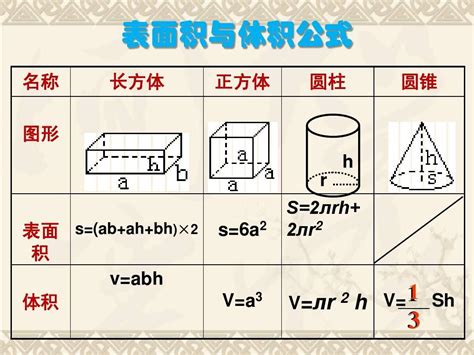 正方体体积计算公式详解资讯攻略01-26
正方体体积计算公式详解资讯攻略01-26 -
 笔记本电脑打字变数字的奥秘与快速解决方案资讯攻略11-19
笔记本电脑打字变数字的奥秘与快速解决方案资讯攻略11-19












