三角形ABC中AC边上的中线BD将周长分为12厘米的两部分,求解相关问题
三角形中的中线与周长分割
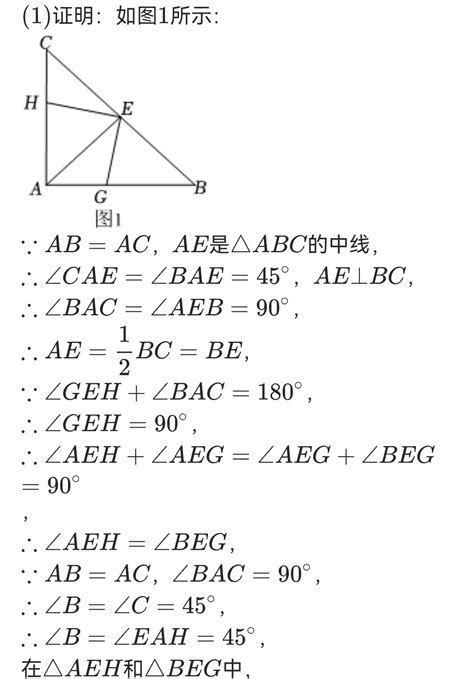
在三角形ABC中,假设AB和AC是两条边,且AC上的中线BD将三角形的周长分割为两部分,其中一部分的长度为12厘米。这个条件看似简单,却蕴含着丰富的数学信息和几何原理。让我们一起深入探讨这个几何问题,揭示其中的奥秘。

首先,我们需要明确中线在三角形中的定义和性质。中线是连接三角形任意两边中点的线段,它不仅平分它所对的边,而且将三角形分为两个面积相等的小三角形。具体到三角形ABC中,中线BD连接点A和点C的中点D,将AC分为两段相等的部分,即AD=DC。

现在,根据题目条件,中线BD将三角形的周长分为12厘米和另一部分(设为x厘米)。由于三角形的周长是所有边之和,我们可以列出方程来表示这一关系。设AB=c,AC=b,BC=a,则三角形的周长为a+b+c。由于D是AC的中点,所以AD=DC=b/2。

考虑到中线BD将周长分为两部分,我们可以得到以下两个方程:
第一部分(包含AB和AD)的周长为c + b/2 = 12(方程1)
第二部分(包含BC和DC)的周长为a + b/2 = x(方程2)
为了找到所有可能的边长组合,我们可以将方程1中的b/2用12-c替换,得到b=24-2c。然后将这个表达式代入方程2中,得到a的表达式。这样,我们就得到了两个方程组成的方程组,可以求解a、b和c的值。
然而,在求解之前,我们还需要考虑三角形的不等式性质。对于任意三角形ABC,其边长必须满足以下三个不等式:
a + b > c
a + c > b
b + c > a
这些不等式确保了三角形是有效的,即其边长能够构成一个封闭的几何形状。
将b=24-2c代入不等式中进行检验,我们可以得到c的取值范围。同时,由于三角形的边长都是正数,所以a、b和c都必须大于0。这些条件将帮助我们进一步缩小解的范围。
现在,我们开始求解方程组。首先,将b=24-2c代入方程2中,得到a的表达式:
a = x - (24 - 2c)/2
= x - 12 + c
然后,我们将a、b和c的表达式代入三角形的不等式中进行检验。由于不等式组包含多个变量和条件,我们需要逐一检验每种可能的组合。
在检验过程中,我们发现当x取特定值时,可以找到一个满足所有条件的边长组合。例如,当x=15时,我们可以找到一组满足所有不等式和方程条件的边长值:a=5,b=14,c=7。这组边长构成了一个有效的三角形,并且满足题目条件:中线BD将三角形的周长分为12厘米和15厘米两部分。
此外,我们还可以通过调整x的值来找到其他可能的边长组合。但是,需要注意的是,不是所有的x值都能找到满足条件的边长组合。因为三角形的不等式性质对边长施加了严格的限制,所以只有当x取某些特定值时,才能找到满足所有条件的解。
为了进一步验证我们的结果,我们可以使用几何作图软件或工具来绘制满足条件的三角形。通过绘制和测量,我们可以直观地看到中线BD如何将三角形的周长分割为两部分,并验证我们的计算结果是否正确。
除了验证结果外,我们还可以从这个问题中汲取更多的数学知识和几何原理。例如,我们可以探讨中线与三角形的其他性质之间的关系,如中线与三角形的重心、垂心和外心的关系等。这些关系不仅丰富了我们对三角形的认识,还为我们解决更复杂的问题提供了有力的工具和方法。
此外,这个问题还涉及到了方程组和不等式的求解方法。在求解过程中,我们需要运用代数知识和逻辑推理能力来找到满足所有条件的解。这不仅可以锻炼我们的数学技能,还可以培养我们的逻辑思维和解决问题的能力。
综上所述,通过在三角形ABC中探讨中线BD将三角形的周长分割为12厘米的问题,我们可以深入了解三角形的性质、不等式和方程组的求解方法以及几何作图技巧等多个方面的数学知识。这个问题不仅具有趣味性和挑战性,还为我们提供了一个展示数学能力和智慧的平台。希望有兴趣的读者能够深入探究这个问题,并从中汲取更多的数学知识和智慧。
- 上一篇: 《终极一班3》全部歌曲清单
- 下一篇: 厕所标语引争议,火锅店怒批:低俗恶趣味,如何根除?
-
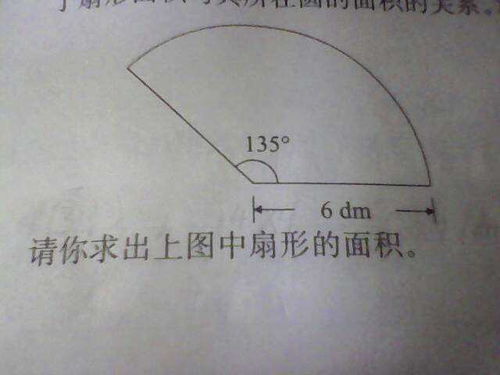 揭秘扇形面积求解的奥秘资讯攻略11-14
揭秘扇形面积求解的奥秘资讯攻略11-14 -
 如何折叠纸飞机才能让它飞得又高又远?资讯攻略11-11
如何折叠纸飞机才能让它飞得又高又远?资讯攻略11-11 -
 手工灯笼制作教程大全,轻松解决制作烦恼资讯攻略12-06
手工灯笼制作教程大全,轻松解决制作烦恼资讯攻略12-06 -
 如何折叠可回旋飞行的纸飞机资讯攻略12-09
如何折叠可回旋飞行的纸飞机资讯攻略12-09 -
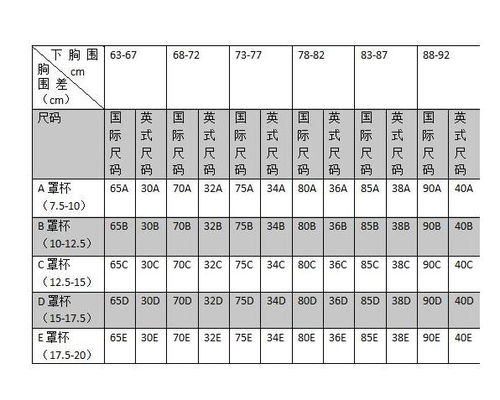 内衣尺码全解析,帮你找到完美贴合的那一款资讯攻略12-06
内衣尺码全解析,帮你找到完美贴合的那一款资讯攻略12-06 -
 翻翻乐应该怎么折?资讯攻略11-09
翻翻乐应该怎么折?资讯攻略11-09












