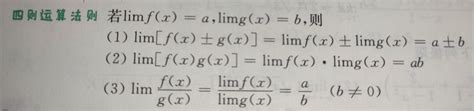揭秘:一次函数fx的表达式及其特性,f(f(x))=x+2求解过程
在数学的世界中,函数作为描述变量之间关系的桥梁,扮演着举足轻重的角色。今天,我们将深入探讨一个具体的数学问题:已知fx是一次函数,且满足f(f(x)) = x + 2的条件,如何求解函数fx的表达式,并进一步判断其性质。

首先,让我们明确一次函数的定义。一次函数,通常表示为f(x) = ax + b(其中a和b为常数,且a ≠ 0),是线性代数中最基本的函数类型之一。它的图像是一条直线,具有明确的斜率和截距,能够简洁地描述两个变量之间的线性关系。

现在,根据题目给出的条件,我们知道fx是一次函数,且f(f(x)) = x + 2。这个等式意味着,当我们先对x应用一次函数fx,然后再对结果应用同一次函数时,所得到的值与x加2相等。这是一个相对复杂的嵌套结构,需要我们逐步拆解和分析。

为了求解fx的表达式,我们可以设fx = ax + b(a ≠ 0)。接下来,我们将fx代入自身,即计算f(f(x)):

f(f(x)) = f(ax + b)
= a(ax + b) + b
= a²x + ab + b
由于题目给出f(f(x)) = x + 2,我们可以将上述表达式与x + 2进行比较,得到方程组:
a²x + ab + b = x + 2
由于这个等式对所有的x都成立,因此我们可以将x的系数和常数项分别相等,得到以下方程组:
a² = 1
ab + b = 2
接下来,我们解这个方程组。首先,从a² = 1可以解得a = 1或a = -1。然后,我们分别考虑这两种情况,并求解对应的b值。
1. 当a = 1时,代入第二个方程ab + b = 2,得到:
b + b = 2
2b = 2
b = 1
因此,在这种情况下,我们得到函数表达式f(x) = x + 1。然而,我们需要验证这个表达式是否满足题目条件。计算f(f(x)):
f(f(x)) = f(x + 1)
= (x + 1) + 1
= x + 2
验证成功!当a = 1,b = 1时,函数f(x) = x + 1确实满足f(f(x)) = x + 2的条件。
2. 当a = -1时,代入第二个方程ab + b = 2,得到:
b + b = 2
0 = 2
这个方程显然不成立,因此a = -1不是有效的解。
综上所述,我们确定了函数fx的表达式为f(x) = x + 1。这个函数具有一些明显的性质:
它是线性函数,图像是一条过点(0,1)且斜率为1的直线。
它是单调递增的,因为斜率a = 1 > 0。
它是奇偶性为“非奇非偶”的函数,因为不满足f(-x) = f(x)或f(-x) = -f(x)的条件。
此外,我们还可以从几何角度理解这个函数。在二维坐标系中,函数f(x) = x + 1的图像是一条与y轴交于点(0,1)、与x轴成45°角的直线。这条直线上的任意一点(x, y)都满足y = x + 1的关系。
最后,回顾整个求解过程,我们发现关键在于正确设立并求解方程组。通过逐步拆解和分析题目条件,我们成功地找到了满足条件的函数表达式,并验证了其正确性。这个过程不仅锻炼了我们的数学思维和解题能力,也让我们对一次函数的性质有了更深入的理解。
在数学探索的道路上,每一个问题都是一次挑战和机遇。通过不断地思考和实践,我们能够逐步揭开数学世界的神秘面纱,发现更多隐藏在数字与符号背后的规律和奥秘。希望今天的探讨能够激发你对数学的兴趣和热爱,让你在未来的学习旅程中更加自信和坚定。
- 上一篇: 美穗子探亲时的情景是怎样的?
- 下一篇: 揭秘《肢解狂魔2》中Mara的扮演者是谁?
-
 求函数值域的常用方法资讯攻略12-06
求函数值域的常用方法资讯攻略12-06 -
 你想知道的fx成员郑秀晶(Krystal)全资料,都在这里!资讯攻略03-31
你想知道的fx成员郑秀晶(Krystal)全资料,都在这里!资讯攻略03-31 -
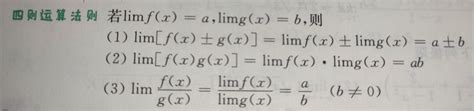 揭秘:极限的四则运算法则详解资讯攻略12-03
揭秘:极限的四则运算法则详解资讯攻略12-03 -
 揭秘!小米商城F码获取攻略大放送资讯攻略01-30
揭秘!小米商城F码获取攻略大放送资讯攻略01-30 -
 小米商城F码:高效获取与巧妙使用方法揭秘资讯攻略12-09
小米商城F码:高效获取与巧妙使用方法揭秘资讯攻略12-09 -
 如何突破极限?全面解析2.44f版攻略秘籍资讯攻略01-30
如何突破极限?全面解析2.44f版攻略秘籍资讯攻略01-30