正方体体积计算公式详解

探秘正方体体积的计算公式：轻松掌握空间几何的奥秘

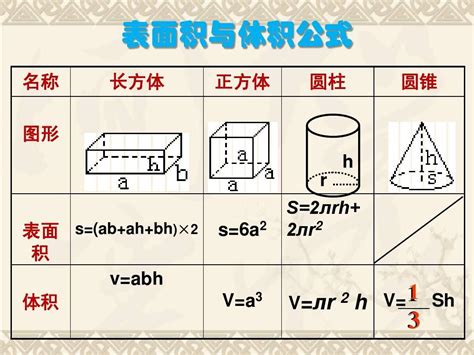
在几何学的奇妙世界里，正方体作为一种独特的三维形状，不仅以其简洁、对称的美感吸引着无数人的目光，更在日常生活和科学研究中发挥着不可或缺的作用。你是否曾经好奇过，这个看似简单的立方体究竟蕴含着怎样的数学奥秘？尤其是当我们想要知道它的体积时，该如何轻松求解呢？今天，就让我们一同踏上这场探索之旅，揭开正方体体积计算公式的神秘面纱。

一、正方体的魅力初体验

想象一下，你手中握着一个由六个完全相同的正方形面围成的立体图形，每一个面都像是精心雕琢的艺术品，既规则又和谐。这就是正方体，一个所有棱长都相等的特殊长方体。它不仅在数学上占据着重要地位，更是建筑设计、艺术创作乃至日常用品设计中的常客。从儿童的积木玩具到现代建筑的立方体结构，正方体的身影无处不在，以其独特的魅力装点着我们的世界。

二、体积：空间的量化艺术

在探讨正方体体积之前，让我们先来理解一下“体积”这个概念。体积，简单来说，就是三维空间中一个物体所占的空间大小。它是衡量物体占据空间多少的一种量度，不同于二维的面积，体积是三维的、立体的。对于正方体而言，它的体积就是其内部空间的大小，而计算这个大小的关键，就在于那个简单而又神奇的公式。

三、揭秘正方体体积的计算公式

那么，正方体体积的计算公式是什么呢？答案出乎意料地简洁：体积V = a³，其中a代表正方体的棱长。这个公式看似简单，却蕴含了深刻的数学原理。想象一下，如果你把一个正方体切成无数个大小相同的小正方体，每个小正方体的体积都是a³（因为每个小正方体的棱长也是a），那么整个大正方体的体积就是这些小正方体体积的总和。由于大正方体是由n×n×n（n为棱长a上的小正方体数量）个小正方体组成，因此总体积就是n³×a³/a³ = a³，这里的n实际上就等于a（因为每个方向上都恰好有a个小正方体）。

四、公式的推导：从直观到抽象

虽然上述解释基于一种直观的想象，但数学总是追求严谨和证明。我们可以通过积分、几何构造或是直接利用长方体的体积公式（长×宽×高）来推导正方体的体积公式。由于正方体的长、宽、高都相等，均为a，所以其体积V = a × a × a = a³。这个推导过程不仅加深了我们对正方体体积公式的理解，也让我们领略到了数学中从具体到抽象、从直观到严谨的魅力。

五、公式的应用：生活中的智慧

掌握了正方体体积的计算公式，我们就可以在生活和工作中灵活运用它来解决实际问题。比如，在装修房屋时，如果需要计算一个正方体储物柜的容量，只需测量其棱长，然后代入公式即可轻松得出。又比如，在物流运输中，了解货物的体积对于合理安排装载空间、优化运输成本至关重要。此外，在工程设计、农业科学、航空航天等领域，正方体体积的计算也是不可或缺的一部分。

六、公式的延伸：多维空间的思考

正方体体积的计算公式不仅局限于三维空间，它还激发了人们对更高维度空间的思考。在四维空间中，存在一个类似正方体的形状——超立方体（或称四维正方体），其体积的计算同样遵循类似的幂次规律，但复杂度大大增加。这种从三维到四维的推广，不仅挑战了我们的想象力，也推动了数学、物理学乃至整个自然科学的发展。

七、公式的背后：数学文化的传承

正方体体积的计算公式不仅仅是数学上的一个符号，它更是人类智慧的结晶，承载着数学文化的深厚底蕴。从古至今，无数数学家、哲学家、科学家在探索几何学的道路上，都曾与正方体有过不解之缘。从古希腊的毕达哥拉斯学派到文艺复兴时期的达芬奇，再到现代的数学家们，正方体及其体积的计算一直是他们研究的重要对象。这个公式不仅见证了数学的发展历程，也促进了人类对空间、形状、度量等概念的深入理解。

八、结语：让数学成为生活的乐趣

回到最初的问题，正方体体积的计算公式是什么？答案已经揭晓——V = a³。但更重要的是，通过这个公式，我们学会了如何运用数学知识去理解和解决生活中的问题，体验到了数学带来的乐趣和成就感。数学不仅仅是一门学科，它更是一种思维方式，一种探索世界、认识自我的工具。在这个充满无限可能的世界里，让我们带着对数学的好奇和热爱，继续前行，去发现更多未知的美好。

在这场关于正方体体积计算公式的探索之旅中，我们不仅收获了知识，更收获了思考的乐趣和成长的喜悦。希望每一位读者都能在未来的日子里，用数学的眼光去观察世界，用数学的语言去表达生活，让数学成为我们人生旅途中的一道亮丽风景线。