理解轴对称图形与成轴对称的概念
在几何学的浩瀚宇宙中,轴对称图形和成轴对称的图形如同一对璀璨的双子星,它们不仅点缀着数学的天空,更是自然界与人类文明中不可或缺的美学元素。通过对这两种图形的深入探索,我们能够领略到几何学的对称之美,理解其在现实生活与科学研究中的广泛应用。

轴对称图形的奥秘
轴对称图形,简而言之,是指一个图形关于某条直线(称为对称轴)对称。当图形沿对称轴折叠时,两部分能够完全重合。这一特性赋予了轴对称图形独特的视觉美感与结构稳定性。从简单的几何形状到复杂的艺术作品,轴对称图形无处不在,它们以不同的形式展现着自然界的和谐与秩序。

几何形状中的轴对称
在基础几何学中,轴对称图形是学生学习对称概念的重要起点。例如,正方形、长方形、等腰三角形、圆形等都是典型的轴对称图形。正方形的四条边等长,且关于两条对角线及两条中垂线对称;圆形则以其圆心为对称中心,任意经过圆心的直线都可视为对称轴,体现了圆的完美对称性。这些图形的对称特性不仅简化了它们的几何性质分析,也为后续学习更复杂的几何概念打下了坚实的基础。
自然界中的轴对称
自然界中,轴对称图形同样俯拾皆是。从蝴蝶翅膀上精致的图案,到雪花晶莹剔透的晶体结构,再到树叶、花卉的排列布局,都遵循着轴对称的原则。这种对称不仅有助于生物在自然界中的生存(如提高飞行效率、减少能量消耗),也是自然界中美学法则的体现。人类通过观察与学习自然界的轴对称现象,不断将其融入艺术创作与建筑设计中,创造出无数令人惊叹的作品。
成轴对称的图形的魅力
与轴对称图形不同,成轴对称的图形指的是两个或多个图形关于某条直线对称。这些图形本身可能不具备轴对称特性,但当它们以特定方式排列时,能够形成整体的对称美。成轴对称的图形在视觉艺术、建筑设计以及科学研究等领域同样扮演着重要角色。
艺术创作中的成轴对称
在艺术领域,成轴对称的图形被广泛用于绘画、雕塑、平面设计等。艺术家们通过巧妙地运用对称原理,创造出既平衡又富有动感的作品。例如,在文艺复兴时期的绘画中,艺术家们常常利用成轴对称的布局来强调画面的中心主题,增强画面的视觉冲击力与稳定性。此外,在现代建筑设计中,成轴对称的布局也常被用来营造庄重、威严的氛围,如中国的故宫建筑群、法国的凡尔赛宫等,都是成轴对称设计的典范。
建筑设计中的成轴对称
在建筑设计中,成轴对称的布局不仅能够提升建筑物的美观度,还能有效组织空间,增强建筑的功能性。例如,许多教堂、宫殿、政府大楼等公共建筑都采用成轴对称的设计,这不仅体现了建筑师的审美追求,也反映了当时社会的文化价值观与权力结构。此外,成轴对称的布局还有助于建筑在视觉上与环境相融合,形成和谐统一的景观效果。
轴对称与成轴对称的科学意义
除了美学价值,轴对称与成轴对称在科学研究中也具有重要意义。它们不仅是物理学、化学、生物学等领域中常见的自然现象,也是解决科学问题的重要工具。
物理学中的应用
在物理学中,轴对称与成轴对称的概念被广泛应用于场论、波动理论、力学等分支。例如,在研究静电场时,常假设电荷分布具有轴对称性,以简化电场强度的计算;在波动理论中,利用对称性原理可以分析波的传播特性与反射规律;在力学中,轴对称结构(如圆柱体、球体)的受力分析与应力分布计算也依赖于对称性原理。
化学中的对称性
化学中,分子的对称性不仅影响着其物理性质(如熔点、沸点、溶解度等),还与其化学活性密切相关。具有轴对称或成轴对称结构的分子往往表现出特定的光谱特性与反应活性。此外,在晶体学中,晶体的对称性是研究其内部结构、生长机制及物理性质的重要基础。
生物学中的对称之美
生物学中,轴对称与成轴对称现象同样普遍存在。从细胞的分裂过程到生物体的形态结构,对称性都发挥着重要作用。例如,许多植物的叶片、花朵以及动物的肢体排列都遵循着轴对称或成轴对称的原则。这种对称性不仅有助于生物体的生长发育,也是其适应环境、提高生存能力的重要策略。
结语
综上所述,轴对称图形与成轴对称的图形不仅是几何学中的基本概念,更是连接数学、物理学、化学、生物学等多个学科的桥梁。它们以独特的对称之美,装点着自然界与人类文明的每一个角落。通过对这些图形的深入探索,我们不仅能够领略到自然界的奇妙与和谐,还能更好地理解科学原理,激发创新思维。在未来的科学研究与艺术创作中,轴对称与成轴对称的概念将继续发挥重要作用,引领我们走向更加美好的明天。
- 上一篇: 淘宝卖家信誉度,轻松几步即可查看!
- 下一篇: 如何让QQ主面板皮肤透明度随心所欲?
-
 轴对称图形与轴对称:区别与内在联系概述资讯攻略03-31
轴对称图形与轴对称:区别与内在联系概述资讯攻略03-31 -
 地方税种概览资讯攻略04-17
地方税种概览资讯攻略04-17 -
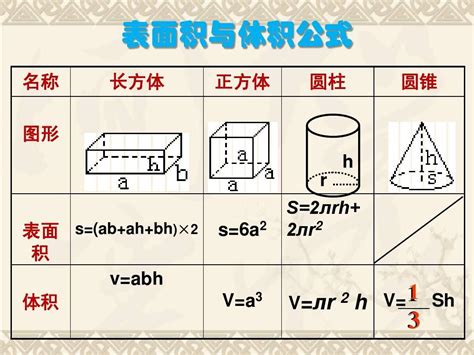 正方体体积计算公式详解资讯攻略01-26
正方体体积计算公式详解资讯攻略01-26 -
 如何简单又好看地画出北京天安门?资讯攻略11-29
如何简单又好看地画出北京天安门?资讯攻略11-29 -
 揭秘第五人格双监管者模式:实战技巧与策略全解析资讯攻略12-07
揭秘第五人格双监管者模式:实战技巧与策略全解析资讯攻略12-07 -
 股票停牌时长解析资讯攻略11-12
股票停牌时长解析资讯攻略11-12












