轴对称图形与轴对称:区别与内在联系概述
轴对称图形与轴对称,这两个概念在数学与艺术领域中频繁出现,却常常让人感到既熟悉又陌生。它们之间究竟存在着怎样的区别与联系?让我们一起揭开它们的神秘面纱,探索这一对称美学的奥秘。

首先,我们要明确“轴对称图形”与“轴对称”的基本定义。轴对称图形,简而言之,是指一个图形关于某条直线(称为对称轴)对称,即图形上的每一点关于这条直线都有对称点,且这些对称点与原图形上的点构成的图形完全相同。换句话说,如果我们沿着对称轴折叠轴对称图形,两部分会完全重合。生活中,轴对称图形的例子不胜枚举,如蝴蝶的翅膀、树叶的脉络、建筑的外观等,它们都以完美的对称展现出大自然的和谐与秩序。

而“轴对称”,则更多地被看作是一种变换关系或性质。它描述的是两个图形(或同一图形的两部分)关于某条直线的对称关系。这里的“轴”同样是指对称轴,而“对称”则意味着两个图形在形状、大小上完全一致,只是位置相对于对称轴进行了镜像翻转。轴对称不仅限于平面图形,也适用于立体图形,甚至抽象的空间结构。在数学中,我们经常利用轴对称性质来简化问题,如通过镜像对称来构造辅助图形,从而更容易地找到解题线索。
接下来,我们深入探讨轴对称图形与轴对称之间的区别。
1. 概念层面:轴对称图形是一个具体的、已经存在的图形,它本身具有轴对称的性质;而轴对称更多地描述了一种图形间的关系或变换,它并不特指某一个具体的图形,而是两个或多个图形之间的一种对称关系。
2. 表现形式:轴对称图形通过自身的结构展现出对称美,我们可以直接观察到它的对称轴和对称点;而轴对称则需要我们比较两个图形,通过判断它们是否关于某条直线对称来确认这种关系。
3. 应用场景:轴对称图形在艺术设计中常被用来创造平衡和谐的视觉效果,如标志设计、建筑装饰等;轴对称在数学解题中则更多地作为一种解题策略,帮助我们理解和解决问题。
尽管轴对称图形与轴对称在概念和应用上有所不同,但它们之间也存在着紧密的联系。
1. 本质相通:无论是轴对称图形还是轴对称,其核心都在于“对称”这一概念。它们都遵循着对称轴两侧元素一一对应、形状大小相同的规则。这种对称性不仅体现了数学中的严谨与和谐,也是自然界和艺术领域中普遍存在的美学原则。
2. 相互转化:在实际应用中,我们可以将轴对称图形看作是两个关于对称轴对称的部分组成的整体;反之,我们也可以将两个具有轴对称关系的图形看作是一个潜在的轴对称图形被分割成了两部分。这种相互转化的视角有助于我们更灵活地运用轴对称的原理进行创作和解题。
3. 共同价值:轴对称图形与轴对称都承载着丰富的文化内涵和审美价值。它们不仅是数学中的基本概念,也是艺术、建筑、科学等领域中不可或缺的元素。通过探索和利用对称性质,我们可以创造出更加美观、实用的作品,同时深化对自然界和人类社会秩序的理解。
此外,轴对称图形与轴对称在教育领域也发挥着重要作用。在数学教学中,通过引导学生观察和分析轴对称图形和轴对称现象,可以培养他们的空间想象能力和逻辑思维能力。同时,轴对称图形和轴对称也是美学教育的重要内容之一,它们能够激发学生的审美情趣和创造力,帮助他们在日常生活中发现美、创造美。
值得一提的是,轴对称图形与轴对称不仅在静态的图形中发挥作用,在动态的图形变换和动画制作中也同样重要。例如,在计算机图形学中,利用轴对称原理可以实现图形的镜像翻转、旋转等变换效果,从而制作出更加生动、逼真的动画场景。
综上所述,轴对称图形与轴对称虽然各有侧重,但它们共同构成了对称美学的基石。通过深入理解它们的区别与联系,我们可以更好地欣赏和利用对称性质来丰富我们的生活、提升我们的创造力。无论是在艺术创作中追求完美的对称美感,还是在数学解题中运用对称性质简化问题,轴对称图形与轴对称都将是我们不可或缺的得力助手。让我们在探索对称美学的道路上不断前行,发现更多未知的美好。
-
 理解轴对称图形与成轴对称的概念资讯攻略12-09
理解轴对称图形与成轴对称的概念资讯攻略12-09 -
 揭秘:轻松辨别左联与右联的绝妙技巧资讯攻略01-24
揭秘:轻松辨别左联与右联的绝妙技巧资讯攻略01-24 -
 地方税种概览资讯攻略04-17
地方税种概览资讯攻略04-17 -
 揭秘第五人格双监管者模式:实战技巧与策略全解析资讯攻略12-07
揭秘第五人格双监管者模式:实战技巧与策略全解析资讯攻略12-07 -
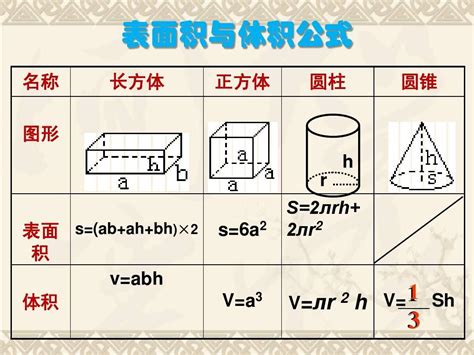 正方体体积计算公式详解资讯攻略01-26
正方体体积计算公式详解资讯攻略01-26 -
 如何简单又好看地画出北京天安门?资讯攻略11-29
如何简单又好看地画出北京天安门?资讯攻略11-29












