揭秘：极限的四则运算法则详解

在数学的广阔领域中，极限理论占据着举足轻重的地位，它不仅是微积分学的基石，也是现代数学分析不可或缺的一部分。极限的四则运算法则，作为处理极限问题的基础工具，对于理解和应用极限概念至关重要。本文将围绕“极限的四则运算法则”展开，详细阐述这些法则的内容、证明过程以及在实际问题中的应用，旨在帮助读者深入理解并掌握这一核心概念。

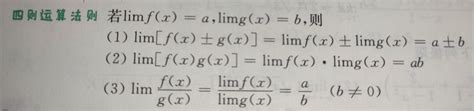
首先，我们需要明确极限的基本定义。在数学分析中，极限描述了一个函数在某一点或无穷远处的行为趋势。具体来说，若函数f(x)在x趋近于某个值a时，其函数值趋近于一个确定的数L，则称L为f(x)在x趋近于a时的极限。这一定义是后续讨论极限四则运算法则的基础。

一、极限的四则运算法则

1. 和的极限法则

若函数f(x)和g(x)在x趋近于a时分别存在极限L和M，则它们的和f(x)+g(x)在x趋近于a时的极限为L+M。这一法则的直观理解是，当两个函数分别趋近于各自的极限时，它们的和也将趋近于这两个极限的和。

证明过程通常依赖于极限的定义和不等式性质。通过构造适当的ε-δ论证，可以证明该法则的正确性。

2. 差的极限法则

与和的极限法则类似，若f(x)和g(x)在x趋近于a时分别存在极限L和M，则它们的差f(x)-g(x)在x趋近于a时的极限为L-M。这一法则同样基于极限的定义和不等式性质进行证明。

3. 积的极限法则

若f(x)和g(x)在x趋近于a时分别存在极限L和M，且其中至少有一个极限不为0（以避免除以0的情况），则它们的积f(x)g(x)在x趋近于a时的极限为LM。这一法则的证明相对复杂，通常涉及到对极限的ε-δ定义的精细操作，以及利用已知极限进行逼近。

4. 商的极限法则

在f(x)和g(x)在x趋近于a时分别存在极限L和M，且M不为0的条件下，它们的商f(x)/g(x)在x趋近于a时的极限为L/M。这一法则的证明同样依赖于极限的ε-δ定义和不等式性质，同时需要特别注意处理分母不为0的情况。

二、极限四则运算法则的应用

极限的四则运算法则在数学分析、物理学、工程学等多个领域都有着广泛的应用。以下是一些具体的应用实例：

1. 在微积分中的应用

在求导数和积分的过程中，极限的四则运算法则起着至关重要的作用。例如，在利用导数定义求函数在某点的导数时，需要用到极限的差商法则；在利用积分定义计算函数在某区间上的定积分时，也需要用到极限的和的法则。

2. 在物理学中的应用

在物理学中，极限的四则运算法则常用于描述物理量的变化趋势。例如，在描述物体在某一时刻的速度、加速度等物理量时，需要用到极限的差的法则；在描述物体在某一时间段内的位移、动量等物理量的累积效应时，则需要用到极限的和的法则。

3. 在工程学中的应用

在工程学中，极限的四则运算法则常用于解决实际问题中的近似计算和误差分析。例如，在结构力学中计算梁的弯曲变形时，需要用到极限的积的法则来近似计算梁的挠度；在电路分析中计算电流、电压等电气量时，则需要用到极限的商的法则来处理电路中的非线性元件。

三、极限四则运算法则的注意事项

虽然极限的四则运算法则非常强大且实用，但在应用过程中也需要注意以下几点：

1. 极限存在性

在应用极限的四则运算法则之前，需要确保所涉及的函数在指定点或无穷远处存在极限。如果某个函数的极限不存在，则不能直接应用这些法则进行计算。

2. 运算顺序

在应用极限的四则运算法则时，需要注意运算的顺序。例如，在计算复杂函数的极限时，可能需要先对函数进行化简或分解，然后再应用极限的四则运算法则进行计算。

3. 特殊情况处理

在处理一些特殊情况时，需要特别注意。例如，在计算商的极限时，需要确保分母不为0；在计算积的极限时，需要避免将极限为0的函数与无穷大相乘等。

四、结语

综上所述，极限的四则运算法则是数学分析中的重要工具之一。它们不仅在数学理论中占据重要地位，而且在物理学、工程学等多个领域都有着广泛的应用。通过深入理解并掌握这些法则的内容、证明过程以及应用方法，我们可以更好地解决实际问题并推动科学的发展。因此，在学习数学分析的过程中，我们应该注重对这些基础知识的理解和掌握，以便在未来的学习和工作中能够灵活运用它们来解决实际问题。